- Dateien hochladen (Bilder/Multimedia/Ton)
- Anzahl der Fragen pro Umfrage
- Umfrage mit MS Word erstellen
- Live-Online-Umfragen bearbeiten
- Umfrageblocks
- Umfrageblock-Randomizer
- Fragen-Randomizer
- Skalenbibliothek
- Monadische Tests
- Sequentielle monadische Tests
- Extraktionsunterstützung für Fragetypen mit Bildauswahl
- Vergleichstest
- Custom validation messages
- Erstellen von Umfragen mit QxBot
- Testing Send
- Survey Preview Options
- Add Questions From a Document
- Survey Authoring 2025
- Online Umfrage erstellen: Standard-Fragetypen
- Erweiterte Fragetypen
- Multiple-Choice-Fragen (Geschlossen)
- Text Frage- Kommentarfeld
- Matrix multi-point scales question type
- Rangordnung
- Smiley-Bewertungsfragen
- Bildfragetyp
- Datum und Uhrzeit Fragetyp
- Captcha-Frage
- Net Promoter Score question type
- Van Westendorp's price sensitivity question
- Auswahlbasierte Conjoint Analyse
- Seite-an-Seite-Matrix
- fragetyp medizin schmerzemfinden studie
- Vorhersage-Antwortoptionen - QuestionPro AI
- Präsentationstext
- Multiple Choice: Wählen Sie eine aus
- Multiple Choice: Wählen Sie viele aus
- Page Timer
- Frage zur Kontaktinformation
- Matrix-Mehrfachauswahlfrage
- Matrix-Tabellenkalkulationsfrage
- Geschlossener Fragetyp - Kartensortierung
- Flex Matrix
- Text Schieberegler - Fragentyp
- Emojis als Bewertung einrichten möglich?
- Rank Order - Drag and Drop
- Bipolare Matrix - Schieberegler
- Bipolare und Likert-Matrix-Fragen
- Gabor-Granger-Preismethode
- Verifizierte Signatur - Fragetyp
- Fragetyp: Sternenbewertung
- Push To Social: Feedback in sozialen Medien “pushen"
- Frage-Dateien hochladen
- Konstantsummen-Fragetyp hinzufügen
- Video-Insights
- Plattform Verbinden
- Rekrutierung von Gemeinden
- TubePulse Videobewertung
- Offener Fragetyp - Kartensortierung
- Map Question Type
- LiveCast
- Antwort-Typ und -Layout
- Fragen nachbestellen
- Frage-Tipps
- Textfeld-Anzeige
- Offene Texteinstellungen für die Kommentar-Box
- Option Sonstiges hinzufügen
- Matrix - Einstellungen
- Bildbewertungsfragen-Einstellungen
- Skalierungsoptionen
- Konstantensumme - Einstellungen
- Standard ausgewählte Option
- Exklusive Optionsvalidierung für Multiple-Choice
- Fragen mit erforderlicher Validierung
- Validierung - Einstellungen
- Validierung entfernen
- Fragenseparatoren
- Fragecodes
- Seitenumbrüche
- Einleitungstext mit Akzeptanz-Kontrollkästchen
- RegEx-Validation
- Verwendung der Fragebibliothek
- Embed Media
- Slider Start Position
- Answer Display Order - Alternate Flip
- Auto-focus für Matrix-Fragen
- Textvalidierungen
- Numeric Input Settings- Spreadsheet
- Antwortgruppen hinzufügen
- Fragen ausblenden
- Mehrere Dateien – Datei anhängen/hochladenj
- Eingabe im Textfeld - Tastaturtyp
- Randomisierung von Antwortoptionen
- Alternate colors
- Conjoint-Analyse - FAQ zur Umsetzung bewährter Verfahren
- Limits für Bilder/Multimedia-Dateien
- Conjoint Prohibited Pairs
- Decimal Separator Currency Format
- Deep Dive
- Logo hinzufügen
- Individuelles Design
- Anzeigeeinstellungen und Umfrage Steuerung
- Automatischer Fragevorschub (Auto-Advance)
- Fortschrittsbalken
- Automatische Fragennummerierung
- Symbolleiste "Soziales Netzwerk"
- Browser-Titel
- Umfrage ausdrucken - Word/PDF-Datei erzeugen
- Navigationsschaltflächen der Umfrage
- Barrierefreies Thema
- Back and Exit Navigation Buttons
- Anzeigemodus - Fokus
- Umfrage Anzeigemodus
- Umfragelayout – Visuell
- Fernseher Integration
- Telly-Integration
- Arbeitsbereich URL
- Klassisches Layout
- Verzweigungs- oder Skip-Logik
- Zusammengesetzte Verzweigungslogik
- Zusammengesetzte oder verzögerte Verzweigung
- Dynamische Quoten-Kontrolle bei Online Umfragen
- Dynamische Text- oder Kommentarfelder
- Extraktionslogik
- Fragen ein- und ausblenden
- Dynamische Show / Hide-Logik
- Bewertungslogik: sofortige Ergebnisanzeige
- Scoring Logik: Net Promoter Score
- Piping-Text (Weiterleitungstext)
- Umfragen verketten
- Schleifenlogik
- Verzweigung zum Beenden der Umfrage
- Logik Operatoren
- Ausgewählte N aus M-Logik
- JavaScript-Logik Syntax-Referenz
- Block-Flow
- Block-Looping
- Syntax-Referenz der Bewertungs-Engine
- Logik "Immer extrahieren" und "Nie extrahieren
- Matrix Extraction
- Gesperrte Extraktion
- Dynamische benutzerdefinierte Variablenaktualisierung
- Erweiterte Randomisierung
- Beispiele für benutzerdefinierte Skripts
- Benutzerdefiniertes Scripting
- Survey Logic Builder - AI
- Befragungseinstellungen
- Sicherheit: Optionen speichern und fortfahren
- Mehrfachabstimmung verhindern
- Schließen, beenden und deaktivieren einer Umfrage
- Admin-Bestätigungs-E-Mail
- Aktionsaufrufe
- Session Timeout bei Online Umfragen
- Abschlussoptionen
- Spotlight-Report
- Antwort ansehen / drucken
- Suchen & Ersetzen
- Einrichten einer Timeout-Option
- Umfragen mehrfach auf einem Gerät ausfüllen
- Text Input Size Settings
- Admin Confirmation Emails
- Datum und Uhrzeit der Umfrage-Schließung
- Standortdaten des Befragten
- Überprüfungsmodus
- Überprüfen, bearbeiten und drucken von Antworten
- Geokodierung
- Fortschrittsanzeige - Dynamischer Stil
- Quotensteuerung | Antworten begrenzen
- Altersüberprüfung
- Umfrageoptionen | Werkzeuge
- Umfrage-Authentifizierung
- Globaler Passwortschutz
- Umfrage-Authentifizierung nur mit E-Mail-Einladungen
- E-Mail Passwort
- Verwendung der Teilnehmer-ID. Login und Sicherheit
- Umfrageauthentifizierung Benutzername/Passwort
- SSL Verschlüsselung
- Facebook-Authentifizierung für Online Umfrage
- Umfrage-Authentifizierung - SAML SSO
- Verschlüsselte Medien-URLs
- Umfrage-URL
- Benutzerdefinierte URL
- E-Mail-Einladungsvorlagen erstellen
- Seriendruck/Personalisierung von E-Mails
- E-Mail-Einstellungen | Absender-Name oder E-Mail
- E-Mail-Listen filtern
- Umfrage-Erinnerungen
- Batch-Export: E-Mail-Listen für externe Verarbeitung
- E-Mail-Status
- spam index online umfragen
- SMS-Einladung erstellen
- Auswertungen von Telefon- und Papier-Umfragen
- Manuelles Hinzufügen von Antworten
- SMS-Preisgestaltung
- Frage in E-Mail einbetten
- E-Mail-Listen löschen
- Mehrsprachiger E-Mail-Verteiler
- Mail-Server-Integration via SMTP Relay
- Antwort-E-Mail-Adresse
- Domain-Authentifizierung
- Fehlerbehebung bei der E-Mail-Zustellung
- QR Code
- E-Mail-Zustellung und Zustellbarkeit
- Offline App Themen
- ${WEB} - Loop-Umfragen
- Mobile App
- Kiosk-Modus
- App-Daten synchronisieren
- Rückmeldung überprüfen / PDF auf Offline-App drucken
- Feld & Geräteprüfung
- Variablen für Offline-Geräte
- Manuelle Synchronisierung von Antworten
- Geräteschlüssel - Details zur Gerätehardware
- Gesichtserkennung im Kiosk-Modus
- Text to Speech
- Push-Benachrichtigung
- Offline-App – Best Practices
- Bericht zum Umfrage-Dashboard
- Teilnehmerstatistiken und Rücklaufquoten
- Drop-Out-Analyse
- Erweiterte Optionen: Banner-Tabelle
- TURF-Analyse
- Trendanalyse
- Korrelationsanalyse
- Umfragenvergleich
- GAP-Analyse
- Mittelwert-Kalkulation
- Gewichteter Mittelwert
- Spinnendiagramm
- Cluster-Analyse
- Dashboard-Filter
- Dashboard - Download-Optionen
- HotSpot-Bild-Tests
- Heatmap Analysis
- Gewichtete Rangfolge
- Antwortoptionen für die Kreuztabellengruppierung
- A/B-Tests in QuestionPro-Umfragen
- Datenqualität
- Antwort für Datenqualitätskennzeichen beenden
- Matrix-Heatmap-Diagramm
- TURF Reach Analysis
- Sicherheit: Passwortgeschützte Umfragen
- Gewichtung - Eliminierung von Stichprobenverzerrungen
- Column proportions test
- Response Identifier
- Conjoint Analysis (Discrete Choice Module) Designs
- Conjoint Teil-Wert-Berechnung
- Conjoint-Analyse - Berechnungen / Methodik
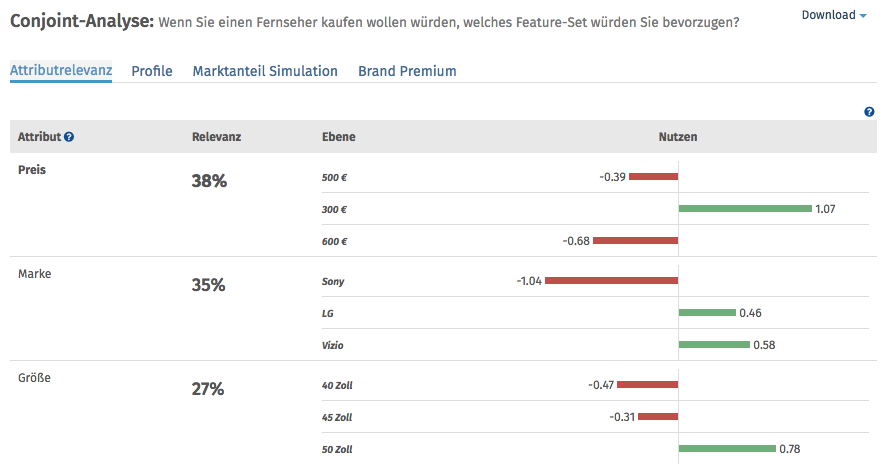
- Conjoint-Analyse - Bedeutung der Attribute
- Conjoint-Profile
- Marktanteil Simulation
- Conjoint-Analyse - Brand Premium
- Was ist MaxDiff Skalierung
- MaxDiff Einstellungen
- Anchored MaxDiff Analysis [BETA-Version]
- MaxDiff FAQ
- MaxDiff- Interpreting Results
- Automatischer E-Mail-Versand von Berichten
- Datenqualität - Gemusterte Antworten
- Datenqualität - gibberish words
- Externe Daten in neue Umfrage importieren
- Download-Center
- Berichte konsolidieren und zusammenfassen
- Befragungsdaten löschen
- Datenqualität - Alle Kontrollkästchen aktivieren
- Berichtexport in Word, Excel und PowerPoint
- Terminplaner
- Datenpad für eine Umfrage
- Merge Data 2.0
- Plagiatserkennung
- Umfrage-Ergebnisse exportieren in SPSS-Format
- Notification Group
- Unselected Checkbox Representation
- IP based location data
- SPSS variable name
- Benutzerprofil aktualisieren
- Zeitzone innerhalb des Umfragekontos ändern
- Geschäftsbereiche
- Organisationsübergreifendes Umfrage Konto
- Nutzungsdashboard
- E-Mail-Adresse für Support-Anfragen
- umfrage software lizenz vergleich
- Log-In - Fehlerbehebung
- Software-Unterstützung
- Welcome Email
- Benutzerrollen und Berechtigungen
- Viele Benutzer gleichzeitig hinzufügen
- Kontobestätigung: Zwei-Faktor-Authentifizierung
- Netzwerkzugang
- Navigating QuestionPro Products
- Changing ownership of the survey
- Unable to access Chat support
- Agency Partnership Referral Program
- Response Limits
- CAN-SPAM-Konformitätstool
- GDPR Compliance
- SAS 70 Typ II Sicherheit
- Sicherstellung der Anonymität der Befragten (RAA)
- Sicherheit
- Einhaltung des kalifornischen Verbraucherschutzgesetzes (CCPA)
- GDPR - right to be Forgotten
- QuestionPro Erklärung zur Zugänglichkeit
- Data Center
- Strong Password
- Automated deletion of data
Conjoint Teil-Wert-Berechnung
Wir verwenden den folgenden Algorithmus zur Berechnung der CBC Conjoint Teil-Werte:
- BEMERKUNG
Sollte es R Befragte geben, mit Individuen r = 1 ... R. Lassen Sie jeden Befragten T Aufgaben sehen, mit t = 1 ... T. Lassen Sie jede Aufgabe t C Konfigurationen (oder Konzepte) haben, mit c = 1 ... C (C ist in unserem Fall normalerweise 3 oder 4).
Wenn wir A-Attribute haben, a = 1 bis A, wobei jedes Attribut La-Stufen hat, l = 1 bis La, dann ist der Teilwert für a ein bestimmtes Attribut/Ebene w'(a,l). Es ist dieses (gezackte Feld) von Teilwerten, für das wir in dieser Übung eine Lösung suchen. Wir können dies zu einem eindimensionalen Feld w(s) vereinfachen, in dem sich die Elemente befinden:
{w’(1,1), w’(1,2) ... w’(1,L1), w’(2,1) ... w’(A,LA)} wobei w S-Elemente hat.Eine spezifische Konfiguration x kann als ein eindimensionales Feld x(s) dargestellt werden, wobei x(s)=1, wenn die spezifische Ebene/Attribute vorhanden sind. Wenn das nicht der Fall ist 0.
Lassen Sie Xrtc die spezifische Konfiguration der c-ten Konfiguration in der t-ten Aufgabe für den r-ten Befragten darstellen. So ist der Versuchsplan die vierdimensionale Matrix X mit der Größe RxTxCxS.
Wenn der Befragte r die Konfiguration c in Aufgabe t wählt, lassen Sie Yrtc=1, sonst ist der Wert 0.
- NUTZEN EINER BESTIMMTEN KONFIGURATION
Der Utility Ux einer bestimmten Konfiguration ist die Summe der Teil-Werte für diejenigen Attribute/Ebenen, die in der Konfiguration, d.h. es ist das skalare Produkt x.w.
- DAS MULTI-NOMIALE LOGIT-MODELL
Für eine einfache Wahl zwischen zwei Konfigurationen, mit den Versorgungseinrichtungen U1 und U2, sagt das MNL-Modell voraus, dass die Konfiguration 1 gewählt wird.
EXP(U1)/(EXP(U1) + EXP(U2)) der Zeit (eine Zahl zwischen 0 und 1).
Bei einer Wahl zwischen N Konfigurationen wird die Konfiguration 1 gewählt.
EXP(U1)/(EXP(U1) + EXP(U2) + ... + EXP(UN)) der Zeit.
- MODELLIERTE WAHLWAHRSCHEINLICHKEIT
Lassen Sie die Auswahlwahrscheinlichkeit (unter Verwendung des MNL-Modells) für die Wahl der c-ten Konfiguration in der t-ten Aufgabe für den r-ten Befragten sein:
Prtc=EXP(xrtc.w)/SUM(EXP(xrt1.w), EXP(xrt2.w), ... , EXP(xrtC.w))
- LOG-WAHRSCHEINLICHKEITSMESSUNG
Das Log-Likelihood-Maß LL wird berechnet als:
Prtc ist eine Funktion des Teil-Wert-Vektors w, der die Menge der Teil-Werte ist, für die wir eine Lösung suchen.
- LÖSUNG FÜR TEIL-WERTE MIT MAXIMALER WAHRSCHEINLICHKEIT
Wir lösen für den Teilwertvektor, indem wir den Vektor w finden, der den Maximalwert für LL ergibt. Beachten Sie, dass wir für S-Variablen lösen.
Hierbei handelt es sich um ein mehrdimensionales nichtlineares kontinuierliches Maximierungsproblem, das eine Standard-Lösungsbibliothek erfordert. Wir verwenden den Nelder-Mead-Simplex-Algorithmus.
Die Log-Likelihood-Funktion sollte als eine Funktion LL(w, Y, X) implementiert und dann optimiert werden, um den Vektor w zu finden, der das Maximum darstellt. Die Antworten Y und der Entwurf X sind gegeben und für eine spezifische Optimierung konstant. Anfangswerte für w können auf den Ursprung 0 gesetzt werden.
Die endgültigen Teilewerte w werden neu skaliert, so dass die Teilewerte für jedes Attribut einen Mittelwert von Null haben, indem einfach der Mittelwert der Teilewerte für alle Ebenen jedes Attributs subtrahiert wird.
Login » Umfragen (wählen Sie eine Umfrage aus) » Analyse » Auswahl-Modellbildung » Conjoint Analyse